Die in der Kurzfassung angewandten Begriffe (Raumwinkel, Strahldichte usw.) sind auch im nachfolgendem ausführlichem Teil erklärt. Für die Langfassung wird Mathematik benötigt. Da das vielen nicht so liegt, ist zwar der ganze Rechenweg gezeigt, aber der Leser braucht nur so tief einzusteigen, wie er es gern möchte, um sich zu überzeugen, daß nicht manipuliert wurde.
Eine plausible Abschätzung des Faktors 4/c (ohne höhere Mathematik) wird wo anders erscheinen.
Aus der Gesamtausstrahlung M folgt die Strahldichte L:
(1) 
Die Energiedichte dU infolge eines Raumwinkelbereiches dΩ ist:
(2) 
Im geschlossenen Hohlraum kommt die Strahlung aus dem vollen Raumwinkel und der ist 4π. Damit wird die Energiedichte U:
(3) 
- Winkelangaben
- Summation (Integration)
- Energieinhalt eines Strahls
Am gebräuchlichsten sind für ebene Winkel (gebräuchliches Formelzeichen φ) die Angaben in ° (φ°). Ein Vollwinkel hat 360°, ein rechter Winkel 90° (1/4 eines Vollwinkels).
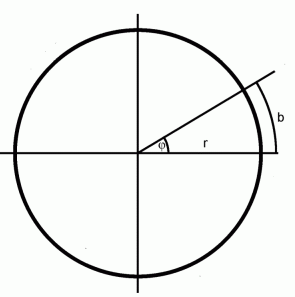
Oft werden die Winkel auch im Bogenmaß (
) angegeben - Angabe in rad (von Radiant). Dabei wird vom Kreis ausgegangen und die Winkelangabe ist das Verhältnis von Bogenlänge b zu Radius r: = b/r. Da der Kreisumfang 2 π r ist, ist das Verhältnis b/r = 2 π r/r = 2 π (Vollwinkel). Ein rechter Winkel ist wieder ein Viertel davon, also π/2.
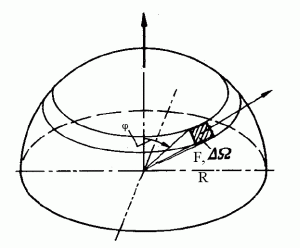
Analog wird ein Raumwinkel Ω definiert - Angabe in sr (von steradiant, der Wortteil "ste" steckt auch in "Stereo"). Statt des Kreises wird von einer Kugel ausgegangen. Der Raumwinkel ist das Verhältnis von einem Stück der Kugeloberfläche F zum Quadrat des Radius R: Ω = F/R2. Da eine Kugel eine Oberfläche von 4 π R2 hat, ist die Größe des Raumwinkels nach allen Richtungen Ω = 4 π R2/ R2 = 4 π. Die Halbkugel hat dementsprechend 2 π.
Die Fläche eines Rechtecks ist leicht zu bestimmen - nämlich Länge mal Breite. Ist die Begrenzungslinie nicht gerade, so ist die Fläche nicht so leicht bestimmbar. Bei einem Kreis mit Radius r ist z.B. die Kreisfläche π r2 - in der Regel einer Formelsammlung entnommen. Damit das in die Formelsammlung aufgenommen werden konnte waren umfangreiche Rechnungen notwendig.
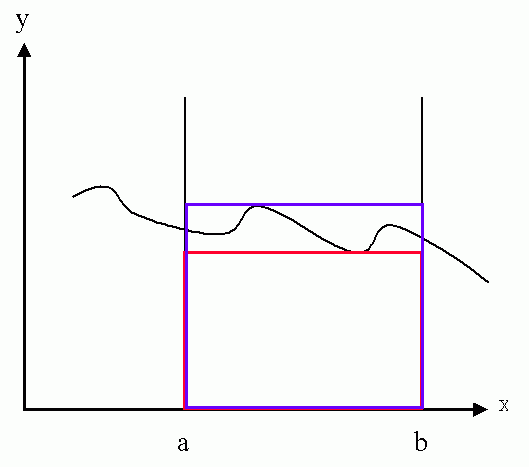
Prinzip dieser Rechnungen. Die eingeschlossene Fläche in dem nachfolgenden Bild ist zu bestimmen. Dabei soll die Kurve durch eine Abhängigkeit y(x) gegeben sein.
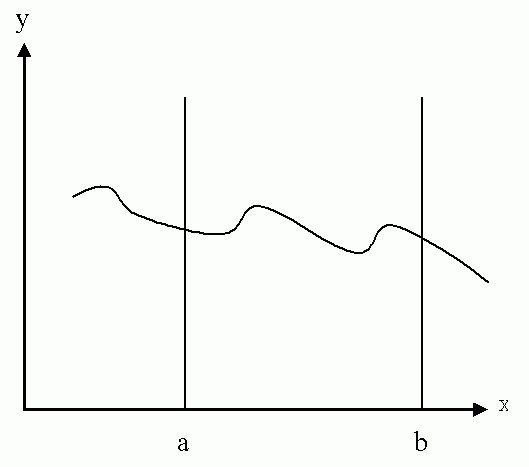
Eine Möglichkeit die eingeschlossene Fläche zu bestimmen besteht darin, die Fläche auszuschneiden und zu wiegen. Durch Gewichtsvergleich mit einem ausgeschnittenen Rechteck (dessen Fläche ja Länge mal Breite ist) kann die Fläche bestimmt werden. Eine zweite Möglichkeit besteht darin (siehe nachfolgendes Bild) ein Gitternetz über diese Fläche zu legen und die Anzahl der Karos zu zählen.
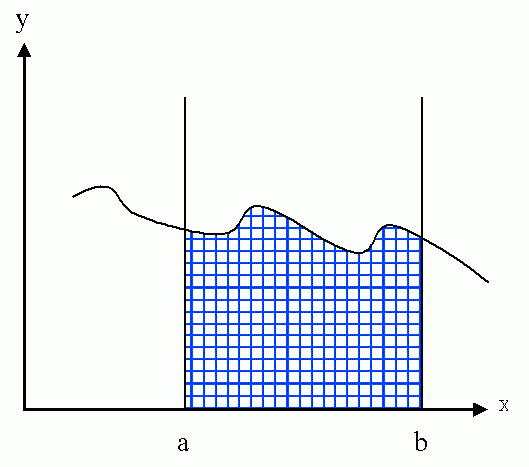
Der Hauptweg die Fläche zu bestimmen ist ein anderer. Erkl&aumml;rung dieses Weges: Ein Rechteck, das vollständig innerhalb der Fläche liegt hat weniger als die gesuchte Fläche, Ein Rechteck, in dem die gesuchte Fläche vollständig innerhalb liegt, hat eine Fläche, die größer als die gesuchte Fläche ist.
Um näher an die gesuchte Fläche zu kommen, wird die gesamte Fläche in Teilabschnitte (Intervalle Δx) unterteilt und für jeden Teilabschnitt jeweils ein Rechteck genommen, das innerhalb der Teilfläche liegt, bzw. ein Rechteck, in dem die Teilfläche liegt. Wenn jeweils alle Teilflächen (innerhalb oder teilweise außerhalb) addiert (summiert) werden, erhält man 2 Summen, von denen die eine kleiner, die andere größer als die gesuchte Fläche ist.
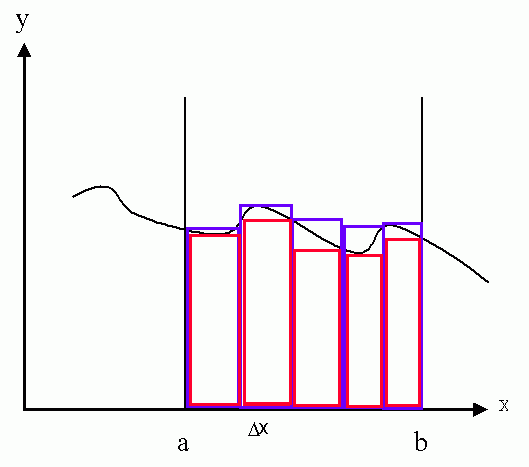
Durch feinere Unterteilung werden sich größere und kleinere Summe immer weniger unterscheiden - und bei ganz feiner Unterteilung praktisch gleich werden. Bei ganz feiner Unterteilung wird Δx als dx bezeichnet (für x können auch andere Formelbuchstaben stehen). Dieser Weg in die ganz feine Unterteilung wird als Grenzwert bezeichnet. Dieser Grenzwert wird als Integral bezeichnet (Formelzeichen 
). Dabei wird auch mit die Grenzen angegeben, zwichen denen die Fläche bestimmt werden soll. Damit lautet die komplette Darstellung:
(4) 
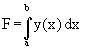
Wenn die funktionelle Abhängigkeit y(x) z.B. eine Fläche darstellt, verkörpert die Fläche, die die Kurve einschließt ein Volumen und dementsprechend ist das Integral ein Volumen.
Am Besten kann man sich das vielleicht analog zu einem Schlauch vorstellen. Der Wasserzähler zeigt an, wieviel Liter Wasser je Sekunde in den Schlauch fließen - und genau so viel Liter je Sekunde kommen aus dem Schlauch heraus. Dem Wasserfluß (l/s) entspricht bei elektromagnetischer Strahlung die Leistung (W). In beiden Strahlen (Wasser bzw. Strahlung) weiß man zunächst nicht, wieviel Wasser im Schlauch bzw. Energie im Strahl ist. Beim Wasser ist aber ein einfacher Trick möglich: man spritzt am Schlauchanfang etwas Farbstoff in das Wasser und mißt die Zeit bis das gefärbte Wasser am Schlauchende ankommt. Solange das gefärbte Wasser noch nicht aus dem Schlauch austritt, wird das einströmende Wasser nur das im Schlauch vorhandene Wasser ersetzen. Wenn die Ersetzung vollständig ist kommt das gefärbte Wasser. Damit ergibt Wasserstrom mal Zeitdauer (bis das gefärbte Wasser ankommt) die Wassermenge, die im Schlauch vorhanden ist.
Wenn der Schlauch durchsichtig ist, kann man auch sehen, wie der gefärbten Wasserpropfen durch den Schlauch wandert. Wenn man die Wanderungsgeschwindigkeit des Propfens mißt und die Schlauchlänge kennt, kann man die Wanderungszeit des gefärbten Propfens über die Schlauchlänge ausrechnen.
Bei elektromagnetischer Strahlung (im sichtbaren Bereich Licht) ist die Ausbreitungsgeschwindigkeit bekannt: die Lichtgeschwindigkeit c. Für einen Strahl mit der Länge L, der eine Leistung N transportiert ergibt sich damit der Energieinhalt E des Strahls:
(5) 
Die Ausstrahlung eines idealen Körpers ist:
(6) 
oder eine entsprechende Dichte 
bzw. 
Wie groß ist die Ausstrahlung L senkrecht zur strahlenden Fläche in den Raumwinkel?
In welchen maximalen Raumwinkel kann die Ausstrahlung erfolgen? Natürlich nur in den Halbraum über der strahlenden Fläche. Begründung: Da nach dem Kirchhoffschen Gesetz der Emissionskoeffizient gleich dem Absorptionskoeffizienten ist, ist es beim idealen schwarzen Körper ganz einfach, da jede Ausstrahlung, die in den Halbraum unter der ausstrahlenden Fläche des den strahlenden Körper erfolgen würde in den Körper selbst erfolgt. Dort wird aber beim ideal schwarzen Körper jede Strahlung vollständig absorbiert . Eine Ausstrahlung, die in diesen Halbraum erfolgen würde spielt deshalb keine Rolle. Deshalb kann man die Ausstrahlung in diesen Halbraum unter der strahlenden Fläche betrachten oder nicht - es spielt keine Rolle.
Wenn eine flache Scheibe betrachtet wird, so ist an der Unterseite (ganz gleich wie dünn die Scheibe ist) eine weitere Oberfläche, die ebenfalls ausstrahlt.
Anmerkung: wenn der strahlende Körper durchscheinend ist, ändert das ebenfalls nichts prinzipiell. Wenn der Körper durchscheinend ist, erfolgt die Ausstrahlung im ganzen Körper und zugleich wird Strahlung im ganzen Körper mehr oder weniger absorbiert. Die Strahlung die auf einer Seite austritt stellt sich als Summe von dem Teil der Strahlung dar, der auf die andere Seite des durchscheinenden Körpers gefallen ist und einem weiteren Teil, der aus der Ausstrahlung des durchscheinenden Körpers selbst stammt. Befindet sich der durchscheinende Körper in einem Hohlraum, der die gleiche Temperatur wie der durchscheinende Körper hat ist die Ausstrahlung gleich dem idealen schwarzen Körper - je nach Dicke ändert sich nur die Anteile von durchgetretener Strahlung und absorbierter Strahlung - jedes andere würde dem 2. Hauptsatz der Thermodynamik widersprechen. Allerdings ist es meßtechnisch unmöglich die Anteile irgendwie nachweisbar zu messen.
Zurück zu einer kleinen strahlenden idealen Fläche. Die Ausstrahlung erfolgt nach allen Richtungen gleich - aber nur mit der in einer betrachteten Richtung zu sehenden Fläche. Das hat ein cos-Gesetz zur Folge. Der cos ist eine Winkelfunktion. Ein Strahler mit diesen Eigenschaften heißt Lambert-Strahler. Zur Illustration wird eine rotationssymmetrische Anordnung betrachtet mit der kleinen strahlenden Fläche F. Die nachfolgende Abbildung zeigt einen Querschnitt.
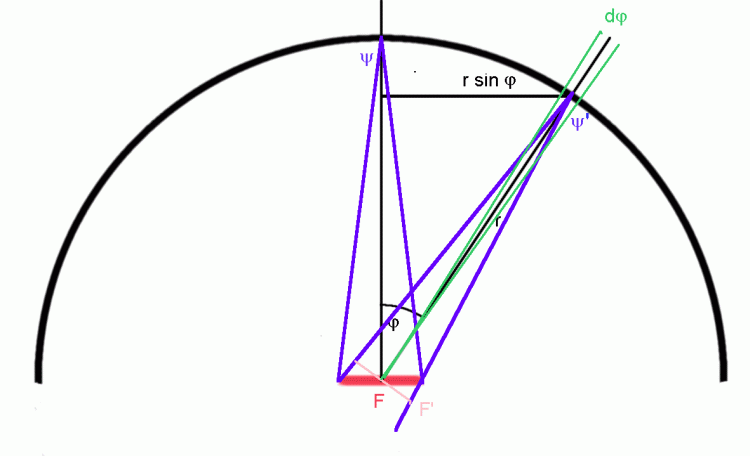
Die Gesamtsumme N = M × F der Strahlung verteilt sich auf den Halbraum. Da die Strahlung in Richtungen, die von der Senkrechten auf der strahlenden Fläche abweichen, geringer ist, muß die Strahlungstärke L im Raumwinkel in Richtung der Senkrechten am Größten sein und größer sein, als wenn die Gesamtstrahlung im ganzen Halbraum (Raumwinkel 2 π) gleichmäßig verteilt wäre. Deshalb gilt:
(7) 
Um den Wert von L genauer zu bestimmen, muß die Ausstrahlung über alle Richtungen integriert werden. Auf der Halbkugel werden Streifen betrachtet. Die Dicke jedes Streifens ist r dφ, die Länge jedes Streifens der Umfang
(8) Uφ = 2 π r sin φ
des zugehörigen Kreises mit dem Radius r sin φ. Gleichzeitig sieht man vom Streifen aus die Fläche immer kleiner, je größer φ ist. Das bedeutet, wenn man die Ausdehnung der strahlenden Fläche von der Senkrechten unter einem Winkel ψ sieht, sieht man die Fläche bei φ > 0 unter einem kleineren Winkel ψ'. Wenn der Betrachter in der Zeichenebene vom Streifen zur strahlenden Fläche schaut, sieht er eine geringere Ausdehnung in der Zeichenebene und zwar ist die Verkürzung proportional cos φ. Senkrecht zur Zeichenebene wird die tatsächliche Ausdehnung gesehen. Damit wird die gesehene Fläche:
(9) F' = F cos φ
Um die gesamte Ausstrahlung zu betrachten, müssen alle Winkel im rechten Winkels zwischen 0 und π/2 betrachtet werden - und das führt zu einem Integral:
(10) 
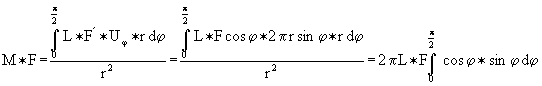
Nach dem Kürzen von F wird:
(11) 
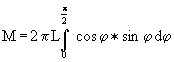
Der cos φ ist immer kleiner als 1. Ohne den cos φ wird die rechte Seite der Gleichung (11) nur größer und das Integral hat den Wert 1, so daß Gleichung (7) entsteht. Mit dem cos φ hat das Integral nur den Wert 1/2. Damit wird:
(12) 
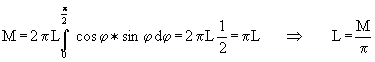
Dazu wird ein beliebig geformter Hohlraum konstanter Temperatur betrachtet, der vollständig geschlossen ist. In diesen Hohlraum wird an einem beliebigen Ort eine gedachte Kugel mit dem Radius r im Abstand R von der Wandung mir r << R betrachtet. Diese Bedingung vereinfacht die Betrachtung, da deshalb alle Strahlen im Kugelbereich als parallel angenommen werden können.
Betrachtet werden kleine Raumwinkelabschnitte dΩH von denen die Strahlung die Kugel durchquert, speziell durch Kreiringe mit dem Radius ρ im Querschnitt der Kugel. Die Breite der Kreisringe soll dρ sein. Diese Betrachtungen werden in der nachfolgenden Zeichnung dargestellt:
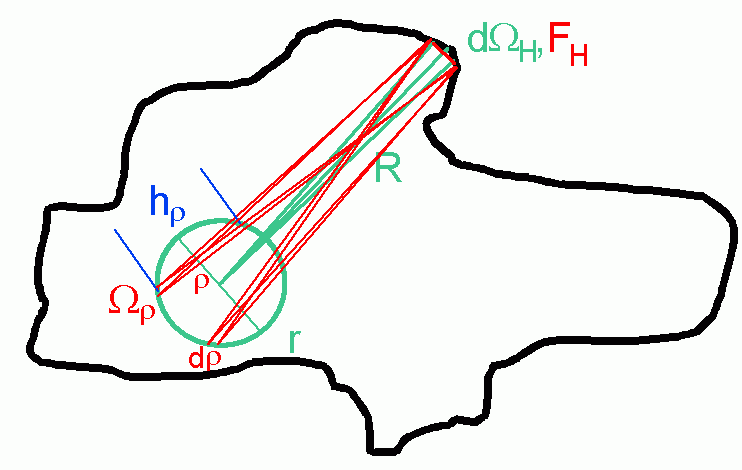
Die betrachtete strahlende Fläche ist FH = R2 d ΩH. Wenn die Senkrechte auf der Hohlraumwandung nicht auf die Kugel zeigt, wird durch d ΩH eine Fläche größer FH betrachtet, aber als strahlende Fläche wirkt nur FH (siehe cos φ in Abschnitt 3).
Von dieser strahlenden Fläche geht ein Teil der Strahlung durch die Kreisringe. Der Umfang Uρ der Kreisringe ist Uρ = 2 π ρ, die Fläche ist Fρ = Uρ d ρ = 2 π ρ d ρ. Der Raumwinkel Ωρ unter dem die Kreisringe von der strahlenden Fläche aus gesehen werden, ist:
(13) 
Die Leistung d N, die durch diese Kreisringe geht, ist:
(14) 
Das Herausfallen von R aus Gleichung (14) zeigt, daß die Entfernung R für die Leistung d N keine Rolle spielt, deshalb darf der Hohlraum eine beliebige Form haben.
Die Strahlen durchqueren das Kugelvolumen, alle Strahlen die einen Kreisring passieren, legen von Eintritt bis zum Austritt die gleiche Strecke hρ zurück. Dazu brauchen sie die Zeit:
(15) 
Die Energie in den Strahlen ist
(16) 
Der letzte Teil von Gleichung (16) (
) stellt ein Volumen V dar: Höhe (
) mal Grundfläche (
). Da die Energie in einem Volumen dividiert durch dieses Volumen die Energiedichte U ergibt (Umfang U und Energiedichte U sind verschiedene Größen), wird:
(17) 
Wie zu sehen ist enthält Gleichung (17) weder ρ noch r, d.h. die Energiedichte ist unabhängig von ρ noch r.
Die Gesamtenergiedichte ergibt sich durch die Summation (Integration) der Anteile in alle Raumrichtungen. Da der Raumwinkel der Vollkugel gleich 4 π ist, wird:
(18) 
Wird in (17) der Wert für L aus Gleichung (11) eingesetzt, wird:
(19) 
Gleichung (19) ist der gesuchte Zusammenhang.